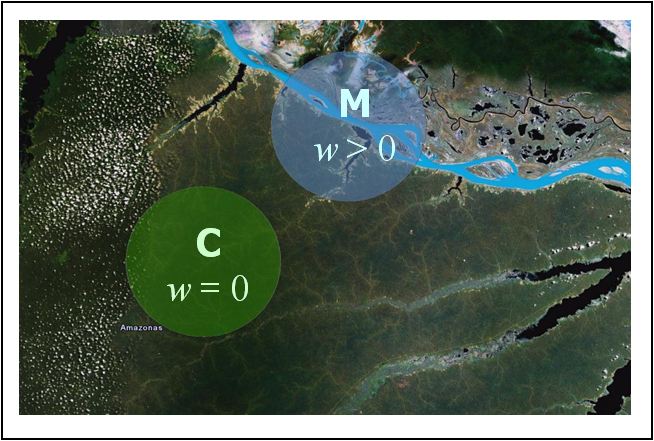
Brakenridge et al (2005) demonstrated that AMSR-E can measure river discharge changes in various climatic conditions. The methodology uses the brightness temperature at 36.5GHz H-polarization during the descending (night) orbit of AMSR-E with a footprint size of approximately 8x12km2 and an average revisit time at 1 day. Brightness temperature is related to the physical temperature T and the emissivity ε of an object: . Due to the different thermal inertia and emission properties of land and water the observed microwave radiation in general accounts for a lower brightness temperature values for water (T_b,water) and higher for land (T_b,land > T_b,water). Since the each observation of the satellite (or pixel) covers a relatively large area of 8x12km2, the observed brightness temperature is mostly composed of both water and land values, in proportion to the relative area of water (w) and land (1 – w) in the pixel.

If the physical temperature remains constant, changes in brightness temperature will be related to changes in water surface extent in the pixel. However, in spite of the great radiation dissimilarity of water and land cover, the raw brightness temperature observations cannot be used to reliably detect changes in surface water area. This is because brightness temperature (T_b) measures are influenced by other factors such as physical temperature, differences in emissivity and atmospheric moisture. While the relative contribution of these factors cannot be measured, the authors assume them to be constant over a larger area. As shown in equation 2, the ratio between two nearby pixel values is a function of w alone. Therefore, by comparing a “wet pixel” received over a river channel of a potential inundation location (w > 0) with a “dry pixel” without water cover (w = 0) the mentioned noise factors can be reduced. The brightness temperature values of the measurement/wet signal are divided by the calibration/dry observations, referred to as M/C ratio or signal s.

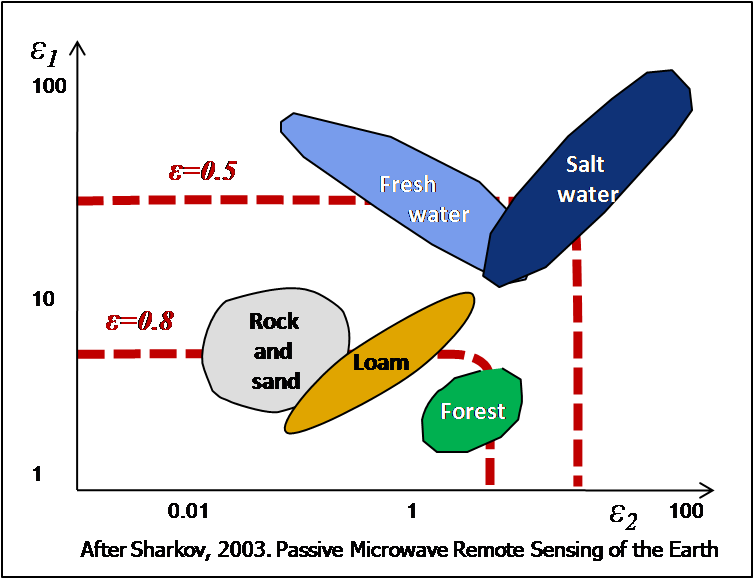Typically, emissivity values of water are around 0.5 and of most minerals between 0.75 and 0.95 (Rees, 1990). When calibration pixels are chosen carefully (without any open water), s varies between 1 (w = 0, no water) and 0.3 to 0.5 (w = 1, fully flooded) depending on the mineral content of the soil. In a time series, s is expected to vary with changes in water surface. Anomalies of the signal s can be correlated well with flood events. Moreover, as demonstrated by Brakenridge et al. (2007), if gauging data is available for the site, the signal can be calibrated to staging height with accurate results.

De Groeve and Riva (2009) showed that a local maximum in a moving window can be used for the calibration value, avoiding the need for manual selection of the calibration site. This finding makes the method applicable in any arbitrary area on Earth, rather than in carefully chosen sites, opening the way for a global flood detection system.

The methodology has been tested with AMSR-E data and TRMM data. However, TRMM data is only available up to latitudes of 50 degrees. In order to have global coverage, AMSR-E data is used.

The data used is the Level 1 brightness temperature at 36.5GHz H-polarization during the descending (night) orbit of AMSR-E with a footprint size of approximately 8x12km2 and an average revisit time of 2 days south of 30 degrees and 1 day north of 30 degrees latitude. The swath data is available about 4h after acquisition by the satellite from the Japanese Space Agency (Jaxa).

The data is downloaded at JRC, resampled (using a nearest neighbor approach) and mosaicked in daily grids with global coverage (see De Groeve and Riva, 2009 for a detailed description of the data processing steps). The result is global grid (4000 by 2000 pixels) of brightness temperature data, available by date. The data of the current day is recalculated whenever new swath data is available.

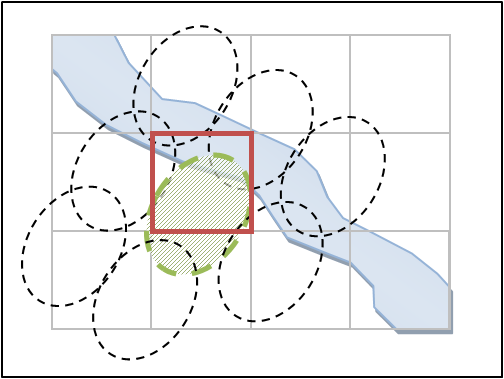
Flood signals are calculated as soon as new data is available. Using the local 95 percentile in a window of 7x7 pixels as the calibration temperature, the signal (M/C value) is calculated for each pixel, resulting in a “signal image”.

In order to distinguish between areas with permanent water (e.g. lakes or wide rivers) and areas with flood waters, we look at change in flood signal over time. Based on a time series of 7 years (going back to June 2002 when the satellite was launched), anomalies are automatically detected using a method described in De Groeve et al. (2006). Since lower M/C signals generally accounts for increased water coverage, extreme events, or major floods, should represent negative anomalies in the time series of a given site. In order to detect anomalies, they first determined the reference value for normal flow, which varies for each site based on the local emissivity properties and river geometry. This reference value was calculated as the average M/C value for the site since the launch of the satellite. They then set flood level thresholds based on the statistics of the time series. Flood magnitude was defined as the number of standard deviations (sd) from the mean (avg):

<

Floods appear typically for anomalies of 2 (small and regular flood) or 4 (large and unusual flood). This is equivalent to probabilities of 2.1% and 0.003%.

With the signal images, a similar method can be applied. However, because no calibration site is necessary, the magnitude can be calculated for any arbitrary point or area. To observe an area, we define an observation area as a collection of pixels. For these observation areas, a set of quantities are calculated including: average magnitude, maximum magnitude, number (an percentage) of pixels exceeding magnitude 2 and number (and percentage) of pixels exceeding magnitude 4.

All these quantities are indicative of the size of the flood in the observation area. The average or maximum magnitude is an objective measure of the degree of flooding, while the pixel count is a measure of the extent of the floods. Since each pixel represents an area of 100km2, the “number of pixels exceeding magnitude 4” are an approximate measurement of the flooded area (number of pixels x 100km2).